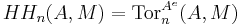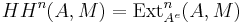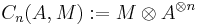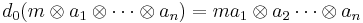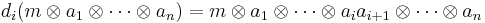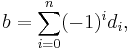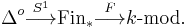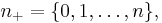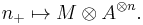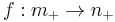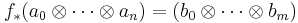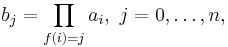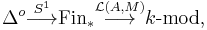Hochschild homology
In mathematics, Hochschild homology (and cohomology) is a homology theory for associative algebras over rings. There is also a theory for Hochschild homology of certain functors. Hochschild cohomology was introduced by Gerhard Hochschild (1945) for algebras over a field, and extended to algebras over more general rings by Cartan & Eilenberg (1956).
Contents |
Definition of Hochschild homology of algebras
Let k be a ring, A an associative k-algebra, and M an A-bimodule. The enveloping algebra of A is the tensor product Ae=A⊗Ao of A with its opposite algebra. Bimodules over A are essentially the same as modules over the enveloping algebra of A, so in particular A and M can be considered as Ae-modules. Cartan & Eilenberg (1956) defined the Hochschild homology and cohomology group of A with coefficients in M in terms of the Tor functor and Ext functor by
Hochschild complex
Let k be a ring, A an associative k-algebra that is a projective k-module, and M an A-bimodule. We will write A⊗n for the n-fold tensor product of A over k. The chain complex that gives rise to Hochschild homology is given by
with boundary operator di defined by
Here ai is in A for all 1 ≤ i ≤ n and m ∈ M. If we let
then b ° b = 0, so (Cn(A,M), b) is a chain complex called the Hochschild complex, and its homology is the Hochschild homology of A with coefficients in M.
Remark
The maps di are face maps making the family of modules Cn(A,M) a simplicial object in the category of k-modules, i.e. a functor Δo → k-mod, where Δ is the simplicial category and k-mod is the category of k-modules. Here Δo is the opposite category of Δ. The degeneracy maps are defined by si(a0 ⊗ ··· ⊗ an) = a0 ⊗ ··· ai ⊗ 1 ⊗ ai+1 ⊗ ··· ⊗ an. Hochschild homology is the homology of this simplicial module.
Hochschild homology of functors
The simplicial circle S1 is a simplicial object in the category Fin* of finite pointed sets, i.e. a functor Δo → Fin*. Thus, if F is a functor F: Fin → k-mod, we get a simplicial module by composing F with S1
The homology of this simplicial module is the Hochschild homology of the functor F. The above definition of Hochschild homology of commutative algebras is the special case where F is the Loday functor.
Loday functor
A skeleton for the category of finite pointed sets is given by the objects
where 0 is the basepoint, and the morphisms are the basepoint preserving set maps. Let A be a commutative k-algebra and M be a symmetric A-bimodule. The Loday functor L(A,M) is given on objects in Fin* by
A morphism
is sent to the morphism f* given by
where
and bj = 1 if f −1(j) = ∅.
Another description of Hochschild homology of algebras
The Hochschild homology of a commutative algebra A with coefficients in a symmetric A-bimodule M is the homology associated to the composition
and this definition agrees with the one above.
See also
References
- Cartan, Henri; Eilenberg, Samuel (1956), Homological algebra, Princeton Mathematical Series, 19, Princeton University Press, ISBN 978-0-691-04991-5, MR0077480, http://books.google.com/books?id=0268b52ghcsC
- Govorov, V.E.; Mikhalev, A.V. (2001), "Cohomology of algebras", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=C/c023110
- Hochschild, G. (1945), "On the cohomology groups of an associative algebra", Annals of Mathematics. Second Series 46: 58–67, ISSN 0003-486X, JSTOR 1969145, MR0011076
- Jean-Louis Loday, Cyclic Homology, Grundlehren der mathematischen Wissenschaften Vol. 301, Springer (1998) ISBN 3-540-63074-0
- Richard S. Pierce, Associative Algebras, Graduate Texts in Mathematics (88), Springer, 1982.
- Teimuraz Pirashvili, Hodge decomposition for higher order Hochschild homology
External links
- Dylan G.L. Allegretti, The Cohomology of Noncommutative Spaces. An elementary introduction to noncommutative geometry which uses Hochschild homology to generalize differential forms).
- Hochschild cohomology in ncatlab